Publications
Critical exponents of normal subgroups in higher rank (2020)
We study the critical exponents of discrete subgroups of a higher rank semi-simple real linear Lie group $G$. Let us fix a Cartan subspace $mathfrak asubset mathfrak g$ of the Lie algebra of $G$. We show that if $Gamma< G$ is a discrete group, and $Gamma’ triangleleft Gamma$ is a Zariski dense normal subgroup, then the limit cones of $Gamma$ and $Gamma’$ in $mathfrak a$ coincide. Moreover, for all linear form $phi : mathfrak ato mathbb R$ positive on this limit cone, the critical exponents in the direction of $phi$ satisfy $displaystyle delta_phi(Gamma’) geq frac 1 2 delta_phi(Gamma)$. Eventually, we show that if $Gamma’backslash Gamma$ is amenable, these critical exponents coincide.
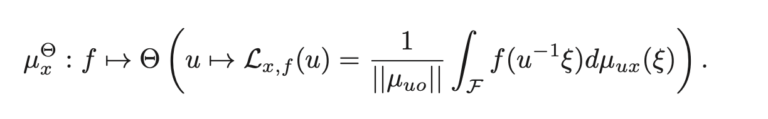
Random triangles on flat tori (2020)
Inspired by classical puzzles in geometry that ask about probabilities of geometric phenomena, we give an explicit formula for the probability that a random triangle on a flat torus is homotopically trivial. Our main tool for this computation involves reducing the problem to new invariant of measurable sets in the plane that is unchanged under area-preserving affine transformations. Our result show that this probability is minimized at all rectangular tori and maximized at the regular hexagonal torus.
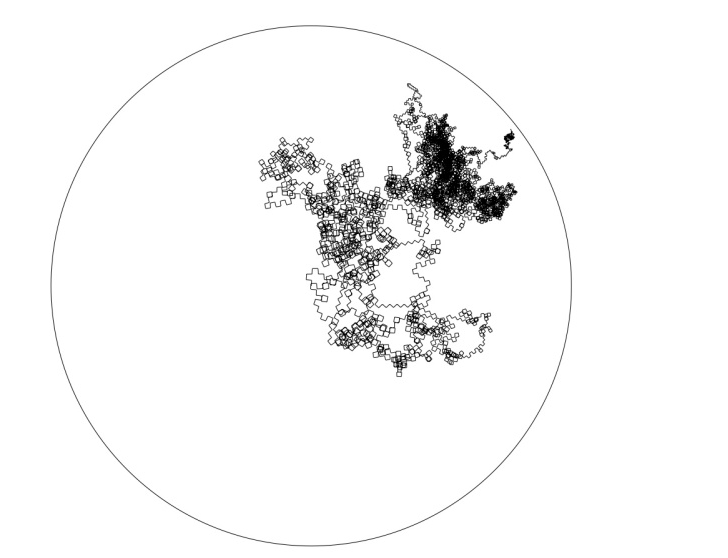
Random path in negatively curved manifolds (2020)
In this article we consider sequences of random points on non-amenable coverings of compact manifolds. The sequences are the successive positions of the trajectories of the Markov process defined recursively by picking a point uniformly on the Dirichlet domain of the previous one. We prove that the escape rate is positive in this setting. The main technical point is to show a non-local isoperimetric inequality from which we get a spectral gap for the Markov operator. In the case where the covering group is Gromov hyperbolic, we deduce that almost all trajectories converge in the Gromov boundary and that the random variables given by the distance from where the process starts satisfy a central limit theorem.
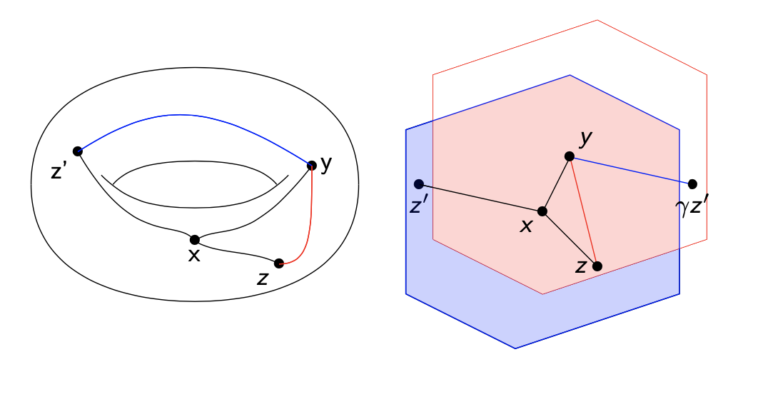
The embedding of the space of negatively curved surfaces in geodesic currents (2019)
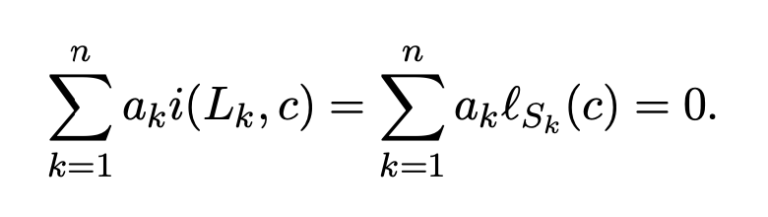
We prove by an algebraic method that the embedding of the Teichmuller space in the space of geodesic currents is totally linearly independent. We prove a similar result for all negatively curved surfaces using an ergodic argument.
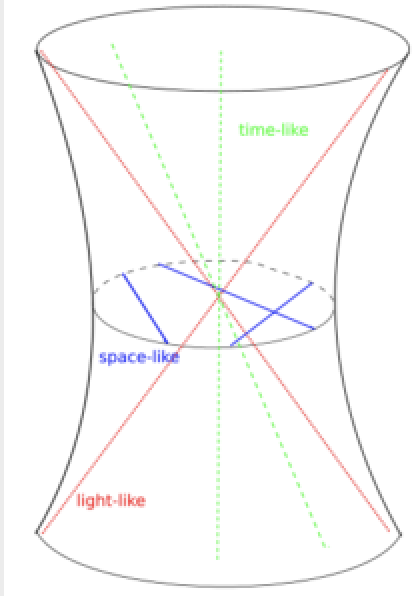
Critical exponent and Hausdorff dimension in pseudo-Riemannian hyperbolic geometry (2019)
The aim of this article is to understand the geometry of limit sets in pseudo-Riemannian hyperbolic geometry. We focus on a class of subgroups of $mathrm{PO}(p,q+1)$ introduced by Danciger, Gu’eritaud and Kassel, called $mathbb{H}^{p,q}$-convex cocompact. We define a pseudo-Riemannian analogue of critical exponent and Hausdorff dimension of the limit set. We show that they are equal and bounded from above by the usual Hausdorff dimension of the limit set. We also prove a rigidity result in $mathbb{H}^{2,1}=mathrm{ADS}^3$ which can be understood as a Lorentzian version of a famous Theorem of R. Bowen in $3$-dimensional hyperbolic geometry.
Hausdorff dimension of limit sets for projective Anosov representations (2019)
Limit sets of $mathrm{AdS}$-quasi-Fuchsian groups of $mathrm{PO}(n,2)$ are always Lipschitz submanifolds. The aim of this article is to show that they are never $mathcal{C}^1$, except for the case of Fuchsian groups. As a byproduct we show that $mathrm{AdS}$-quasi-Fuchsian groups that are not Fuchsian are Zariski dense in $mathrm{PO}(n,2)$.
Regularity of limit sets of AdS quasi-Fuchsian groups (2018)
Limit sets of $mathrm{AdS}$-quasi-Fuchsian groups of $mathrm{PO}(n,2)$ are always Lipschitz submanifolds. The aim of this article is to show that they are never $mathcal{C}^1$, except for the case of Fuchsian groups. As a byproduct we show that $mathrm{AdS}$-quasi-Fuchsian groups that are not Fuchsian are Zariski dense in $mathrm{PO}(n,2)$.
Entropy of embedded surfaces in quasi-fuchsian manifolds (2018)
We compare critical exponent for quasi-Fuchsian groups acting on the hyperbolic 3-space, $mathbb{H}^3$, and on invariant disks embedded in $mathbb{H}^3$. We give a rigidity theorem for all embedded surfaces when the action is Fuchsian and a rigidity theorem for negatively curved surfaces when the action is quasi-Fuchsian.
Topological mixing of the Weyl chamber flow (2018)
We prove that a sequence of quasi-Fuchsian representations for which the critical exponent converges to the topological dimension of the boundary of the group (larger than 2), converges up to subsequence and conjugacy to a totally geodesic representation.
Critical exponent for geodesic currents (2017)
For any geodesic current we associated a quasi-metric space. For a subclass of geodesic currents, called filling, it defines a metric and we study the critical exponent associated to this space. We show that is is equal to the exponential growth rate of the intersection function for closed curves.
Convergence of quasi-Fuchsian groups using critical exponent (2017)
We prove that a sequence of quasi-Fuchsian representations for which the critical exponent converges to the topological dimension of the boundary of the group (larger than 2), converges up to subsequence and conjugacy to a totally geodesic representation.
Counting closed geodesics in globally hyperbolic maximal compact AdS 3-manifolds (2017)
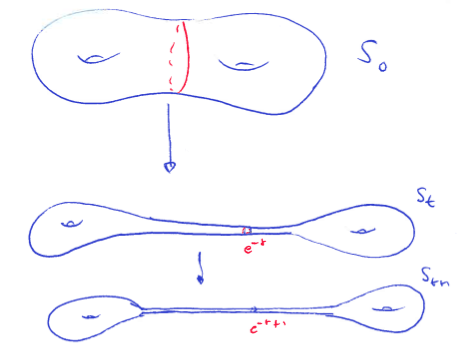
We propose a definition for the length of closed geodesics in a globally hyperbolic maximal compact (GHMC) Anti-De Sitter manifold. We then prove that the number of closed geodesics of length less than $R$ grows exponentially fast with $R$ and the exponential growth rate is related to the critical exponent associated to the two hyperbolic surfaces coming from Mess parametrization. We get an equivalent of three results for quasi-Fuchsian manifolds in the GHMC setting : R. Bowen’s rigidity theorem of critical exponent, A. Sanders’ isolation theorem and C. McMullen’s examples lightening the behaviour of this exponent when the surfaces range over Teichmuller space.